Logistic Regression

(last updated on 2011-02-17)

As usual, Wikipedia's article on logistic regression is a good starting point. This short article provides a practical and quick guide to the application of logistic regression.

 Usage

Logistic regression models the relationship between a binary parameter (i.e. dichotomous, e.g. alive or dead) and other parameters that are assumed to be related. In other words, with a logistic regression model and given predicting parameters, one can predict the probability of a certain event. For example, one can use a logistic regression model to predict the probability of person's death in 5 years based on parameters such as age, gender, smoking time, number of heart attacks, etc.

 Fundamentals

Since most statistical software packages provide all the computations, users usually only need to understand the concepts and some fundamental mathematics behind the logistic regression. The outcome of logistic regression is:

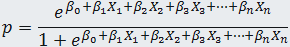
where p is the probability for the event to occur, x_i is a predicting parameter, β₀ is the "intercept",  and β₁ , β₂ , β₃, and so on, are the regression coefficients. The predicting parameters can be metric, binary or ordinal.  In the latter two cases, some transformation will be needed to generate design (i.e. dummy) variables to represent them.

The key element in logistic regression is the logit transformation defined as following:

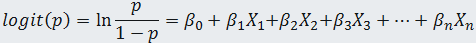
where g(x) =  β₀ + β₀x₀ + β₁x₁ + ... + β_nx_n is called logit. This transformation enables logistic regression to use many mathematical elements of linear regression.  The above equation is also the link function for logistic regression.  Link function yields linear function of the independent variable for the dependent.

Model Building Steps

1. Use univariate analysis (t-test or logistic regression) to select relevant variables.
2. If necessary, assess the linearity of the variables.
3. If necessary, assess the interactions among the selected variables.
4. Build multi-variate model.

One popular deterministic approach to select variables is stepwise logistic regression. It includes backward and forward stepwise logistic regressions.

Assessing the model

The essence of assessing logistic model is the same as that of any other model assessment – comparing the predicted with the observed. They include the following methods:

1. Perrson Chi-square statisitc.
2. Deviance.
3. Hosmer-Lemeshow test that is essentially a variant of Chi-square statistic, but much more practical because in most cases Chi-square test assumptions (e.g. m-asymptotic) are not met.

Model Interpretation

Coefficients β₀ , β₁ , β₂ , β₃, ...β_n  are generated by the regression and each of them(β_i) has its own significance level - p_i.  Just like other statistical analysis, p_i shows whether β_i makes a significant difference from assuming β_i = 0.  There are different ways to assess the significance hence resulting in different p’s, but all of them have the same objective. They just approach it differently. They include deviance test, Wald test and SCORE test. The sign of each estimated coefficient tells whether its corresponding predicting parameter contributes positively or negatively to the occurrence of the event.

This short article was originally written after extensive communication with Robert TV Kung, PhD and Douglas McNair, MD, PhD who were leading an effort to apply logistic regression to a sophisticated medical device clinical trial.